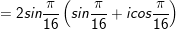Giải Bài Tập Số Phức - Các Dạng Toán Về Số Phức, Cách Giải Và Bài Tập
Số phức là trong số những nội dung quan trọng thường xuất hiện trong đề thi trung học phổ thông Quốc gia. Cũng chính vì vậy teen 2k1 tránh việc bỏ qua bài học kinh nghiệm này để không mất điểm đáng tiếc. Em hãy đọc nội dung bài viết sau của CCBook - Đọc là đỗ nhằm cómẹo giải bài tập số phức 12 siêu cấp tốc giúp em đạt điểm cao môn Toán. Bạn đang xem: Giải bài tập số phức
Các kiến thức trọng trọng tâm giúp emgiải bài xích tập số phức 12 khôn cùng nhanh
Để làm những dạng bài tập số phức khó nhuần nhuyễn em rất cần phải nắm được các kiến thức trọng tâm.

Khái niệm số phức
Số phức gồm dạng z = a + bi, (a, b∈ℜ), trong đó a là phần thực, b là phần ảo, i là đơn vị ảo:i² = - 1
Tập hợp những số phức là C
Nếu a = 0, z = bi được hotline là số thuần ảo
Nếu b = 0 , z = a + 0i được call là số thực
Số 0 vừa là số thực, vừa là số ảo
Số đối của phức z = a + bi là -z = - a - bi
Các phép toán trên tập số phức
Cho hai số phứcz₁ = a + bi,z₂ = c + di.
Hai số phức bởi nhau:

Môđun của số phức, số phức liên hợp
Số phức phối hợp của số phức z = a + bi là

Phương trình trên tập số phức
Căn bậc nhì của số phức:
z = x + yi là căn bậc nhị của số phức

w = 0 tất cả suy nhất 1 căn bậc nhị là z = 0
w≠ 0 gồm hai căn bậc hai
Hai căn bậc nhị của số a > 0 là±

Hai căn bận nhì của số a TỔNG HỢP LÝ THUYẾT TOÁN ÔN THI ĐẠI HỌC TỪ A – Z cho TEEN 2K1
Các dạngbài tập số phức 12 tuyệt và nặng nề cho teen 2k1
Dạng 1: các phép toán bên trên tập phù hợp số phức
Cho số phức z = a + bi không giống 0. Số phức

A.



Hướng dẫn giải:
Ta có:

Do đó phần thực là:

⇒ Chọn giải pháp A.
Dạng 2: tra cứu số phức thỏa mãn nhu cầu điều kiện cho trước
Cho số phức w = 1 + (1 + i) + (1 + i)² + (1 + i)³ ....


A. Phần thực bằng


B. Phần thực bằng


C. Phần thực bằng


D. Phần thực bằng


Hướng dẫn giải bỏ ra tiết:
Ta có:

Suy ra:


Vậy số phức



Chọn phương án B

Dạng 3: Phương trình trên tập thích hợp phức
Gọiz₁ cùng z₂ là hai nghiệm phức của phương trình z² - 2z + 10 = 0.
Tính A =

A. A = 30 B. A = 10 C. A = đôi mươi D. A = 50
Hướng dẫn giải bỏ ra tiết:
Phương trìnhz² - 2z + 10 = 0 cóΔ" = 1 - 10 = -9 = (3i)² yêu cầu phương trình gồm hai nghiệm phức làz₁ = 1 + 3i vàz₂ = 1 - 3i.

Chọn lời giải C
Mẹo giải bài xích tập số phức 12 siêu cấp tốc qua tài liệu chuẩn chỉnh có 1 ko 2
Để giúp các em bao gồm cái nhìn tổng quát nhất về thi trắc nghiệm. Cũng giống như là giải các bài tập nặng nề thường mở ra trong đề thi trung học phổ thông Quốc gia. Uy tín CCBook - Đọc là đỗ với NXB Đại học giang sơn HN đã thành lập cuốn sách Ôn luyện thi trắc nghiệm THPT non sông năm 2019.
Đây chính là cẩm nang nhằm em ôn tập nhuần nhuyễn các dạng bài xích tập số phức 12 và toàn cục các bài bác tập cực nhọc trong chương trình học của tất cả 3 năm.

Ưu điểm tiêu biểu của sách Ôn luyện thi trắc nghiệm THPT quốc gia năm 2019:
Với muc tiêu hỗ trợ kiến thức một cách không thiếu thốn và bỏ ra tiết. Cuốn sách đang tận dụng triệt để những điểm mạnh của sơ đồ vật khối trong việc tổng hợp những kiến thức định hướng ôn luyện quan trọng cho những em:Những con kiến thức định hướng phức tạp sẽ được tổng hợp, đầy đủ, ngắn gọn với dễ nhớ.Kiến thức được trình diễn có hệ thống, giúp ghi nhớ dễ dàng dàng. Không bị lẫn lộn giữa các đơn vị kỹ năng có mối contact hay tương đương trên một phương diện như thế nào đó.Rèn luyện tư duy tiếp cận các đơn vị lý thuyết kiến thức.Sách hỗ trợ cho những em các bài tập chủng loại mới toàn bộ các dạng bài tập tất cả thể gặp mặt và cách thức giải, giải thuật chi tiết. Đặc biệt là phương thức giải nhanh những bài tập cạnh tranh giúp em không còn kinh ngạc trước đều dạng bài xích dù nặng nề đến đâu.Sách có khối hệ thống đáp án và giải đáp giải cụ thể giúp em hiểu cấp tốc và lưu giữ lâu kỹ năng và kiến thức đã họcSách còn tích hợp các tiện ích đi kèm cung ứng tối đa đến em trong vấn đề học
Hệ thống đoạn phim bài giảng:Lý thuyết: Tổng hợp nhấn mạnh nội dung đề xuất chú ý, kim chỉ nan trọng tâm, xâu chuỗi các kiến thức của chuyên đề, chủ thể và chương.
Các bài bác tập từ luyện: cung ứng chữa các bài tập khó, mẹo giải cấp tốc và buổi tối ưu thời gian làm bài.
Hệ thống thi thử CCTest:Với ngân hàng thắc mắc đầy đủ những dạng bài bác thường xuất hiện trong đề thi. Có khá đầy đủ các cường độ từ dễ đến cạnh tranh để em ôn luyện nhuần nhuyễn.
Nhóm giải đáp thắc mắc trên Facebook 24/24:Là chỗ quy tụ các thầy cô giỏi, các thủ khoa giúp em giải đáp đều thắc mắc nhỏ tuổi nhất trong quy trình học tập.
Số phức và những dạng toán về số phức là giữa những nội dung mà nhiều các bạn cảm thấy chúng kha khá trừu tượng với khá cực nhọc hiểu, 1 phần nguyên nhân là họ đã thừa quen với số thực trong những năm học trước.
Vì vậy, ở nội dung bài viết này Hay
Hoc
Hoi.Vn sẽ hệ thống lại các dạng toán về số phức mặt khác hướng dẫn bí quyết giải các dạng bài tập này. Trước khi bắt tay vào giải các dạng bài tập số phức, các bạn cũng đề xuất nhớ các nội dung về lý thuyết số phức.
I. Triết lý về Số phức
1. Số phức là gì?
• Định nghĩa số phức
- Tập hợp số phức:
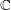
- Số phức (dạng đại số):
(, a là phần thực, b là phần ảo, i là đơn vị chức năng ảo i2 = -1)
♦ z là số thực ⇔ phần ảo của z bởi 0 (b = 0).
♦ z là thuần ảo ⇔ phần thực của z bằng 0 (a = 0).
♦ Số 0 vừa là số thực vừa là số ảo
♦ 2 số phức bởi nhau:
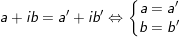
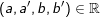
2. Biểu diễn hình học của số phức
- Số phức: , () được biểu diễn bởi điểm M(a,b) tốt bởi
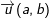

3. Phép cộng, trừ số phức
- cho 2 số phức: , khi đó:
♦
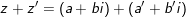
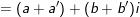
♦
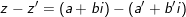
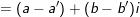
- Số đối của: là
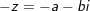
- Nếu
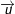
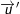
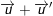
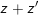


4. Phép nhân 2 số phức
- mang đến 2 số phức: , lúc đó:
♦
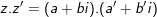
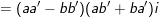
♦
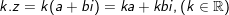
5. Số phức liên hợp
- Số phức phối hợp của số phức
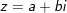
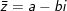
♦
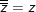
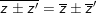
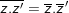
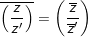
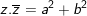
♦ z là số thực ⇔
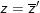
♦ z là số thuần ảo:
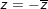
6. Phép phân chia số phức khác 0
♦
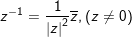
♦
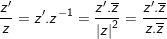
♦
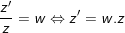
7. Mô-đun của số phức
- mang lại số phức: , thì:
♦
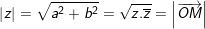
♦
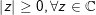
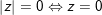
♦
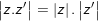
♦
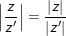
♦
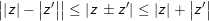
8. Căn bậc 2 của số phức
♦
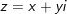


♦ w = 0 tất cả đúng một căn bậc 2 là z = 0
♦ w≠ 0 tất cả đúng 2 cặn bậc 2 đối nhau
♦ 2 căn bậc 2 của a > 0 là
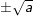
♦ 2 căn bậc 2 của a 9. Phương trình bậc 2 của số phức
- đến phương trình bậc 2 số phức gồm dạng: Az2 + Bz + C = 0, (*) (A,B,C là những số phức mang đến trước, A≠0).
- khi đó: Δ = B2 - 4AC
- Δ ≠ 0, phương trình (*) có 2 nghiệm phân biệt:

- Δ = 0, phương trình (*) có 1 nghiệm kép:
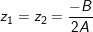
* Chú ý: Nếu
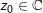
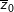
10. Dạng lượng giác của số phức
• z = r(cosφ + isinφ), r > 0 là dạng lượng giác của (z≠0).
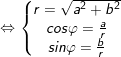
• φ là một trong những acgumen của z, φ = (Ox,OM)
•


11. Nhân phân chia số phức bên dưới dạng lượng giác
- mang lại z = r(cosφ + isinφ) và z" = r"(cosφ" + isinφ")
•
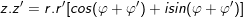
•
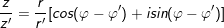
12. Bí quyết Moivre (Moa-vrơ).
•
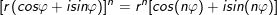
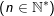
•
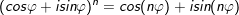
13. Căn bậc 2 của số phức bên dưới dạng lượng giác
• mang đến z = r(cosφ + isinφ), r > 0 tất cả căn bậc 2 là:
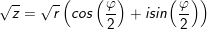
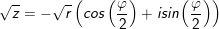
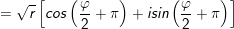
• Mở rộng: z = r(cosφ + isinφ), r > 0 có n căn bậc n là:
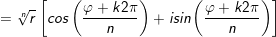
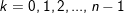
II. Các dạng toán về Số phức và cách giải
• Dạng 1: những phép tính về số phức
* cách thức giải: Vận dụng những công thức Cộng, Trừ, Nhân, Chia, Luỹ vượt và tính chất phép toán của số phức.
- Chú ý: Khi đo lường các số thức hoàn toàn có thể sử dụng hằng đẳng thức như số thực như bình phương của tổng, lập phương của tổng xuất xắc hiệu 2 số phức,...
° Ví dụ 1: cho số phức

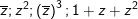
° Lời giải:
+) Ta có:
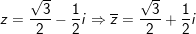
+) Ta có:
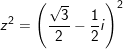
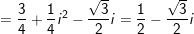
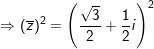
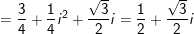
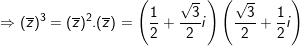
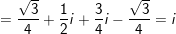
+) Ta có: 1 + z + z2 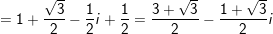
* Tương tự: Cho số phức
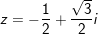
- Ta có:
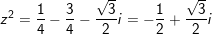
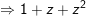
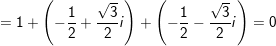
° Ví dụ 2: Tính tổng sau:
a) K = 1 + i + i2 + i3 + ... + i2009
b) M = 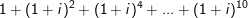
c) N = (1 - i)100
° Lời giải:
a) Ta có: 1 - i2010 = (1 - i)(1 + i + i2 + i3 +...+ i2009)
Mà 1 - i2010 = 1 - (i2)1005 = 1 - (-1) = 1 + 1 = 2.
⇒ K = 1 + i + i2 + i3 +...+ i2009 =
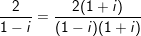
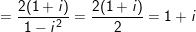
b) M là tổng của 10 số hạng trước tiên của 1 cấp số nhân với số hạng thứ nhất là u1 = 1, bội q = (1 + i)2 = 2i. Ta có:
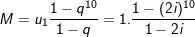
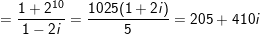
c)
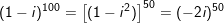
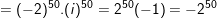
° Ví dụ 3: cho 2 số phức z1, z2 thoả
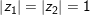
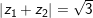
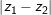
° Lời giải:
- Đặt
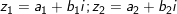
- từ bỏ giải thiết ta có:
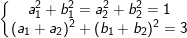
⇒ 2(a1b1 + a2b2) = 1
⇒ (a1 - a2)2 + (b1 - b2)2 = 1
⇒ |z1 - z2| = 1.
• Dạng 2: Tìm số phức thoả điều kiện cho trước (giải phương trình số phức)
* cách thức giải: Vận dụng các đặc điểm của số phức, những phép biến đổi để xử lý bài toán.
Xem thêm: Những Thỏi Son Môi Màu Hồng Phấn Giá Tốt T07/2023, Son Màu Hồng Nhạt Hợp Với Da Nào
° lấy ví dụ 1: tìm số phức z thoả mãn
a)
b)
° Lời giải:
a)

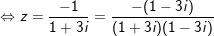

b)

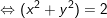
mà
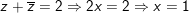
thế x = 1 vào (*) ta được y = ±1.
Vậy số phức bắt buộc tìm là 1 + i và 1 - i.
° Ví dụ 2: Tìm số phức z thoả mãn
a)
b) 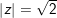
° Lời giải:
a)
- Ta có: 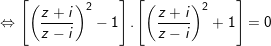
+) TH1:
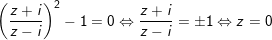
+) TH2:
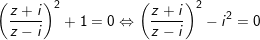
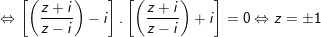
• Dạng 3: xác định phần thực phần ảo, tra cứu đối số, nghịch đảo module, phối hợp của số phức và trình diễn hình học của số phức
* cách thức giải: Dạng này chia thành nhiều loại bài xích toán liên quan tới đặc thù của số phức.
♦ loại 1: tra cứu phần thực phần ảo của số phức
- cách giải: chuyển đổi số phức về dạng z = a + bi, suy ra phần thực là a, phần ảo là b.
° Ví dụ 1: Tìm phần thực phần ảo của số phức sau:
a) z = i + (2 - 4i) - (3 - 5i)
b) z = (-1 + i)3 - (2i)3
c)
° Lời giải:
a) z = i + (2 - 4i) - (3 - 5i) = (2 - 3) + (1 - 4 + 5)i = -1 + 2i
⇒ Vậy số phức sẽ cho có phần thực là -1; phần ảo là 2.
b) z = (-1 + i)3 - (2i)3 = (-1 + i3 + 3i - 3i2) - 8i3 = (-1 - i + 3i + 3) + 8i = 2 + 10i
⇒ Vậy số phức đã cho tất cả phần thực là 2; phần ảo là 10.
c) 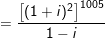
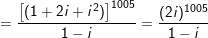
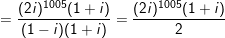
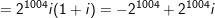
° Ví dụ 2: Tìm phần thực phần ảo của số phức sau:
a) u = z1 - 2z2 cùng với z1 = 1 + 2i; z2 = 2 - 3i
b) v = z1z2 với z1 = 2 + 5i; z2 = 3 - 4i
° Lời giải:
a) u = z1 - 2z2 = (1 + 2i) - 2(2 - 3i) = (1 - 4) + (2 + 6)i = -3 + 8i
⇒ Vậy số phức đã cho bao gồm phần thực là -3; phần ảo là 8.
b) v = z1z2 với z1 = 2 + 5i; z2 = 3 - 4i = (2 + 5i)(3 - 4i) = (6 - 8i + 15i - 20i2) = 26 + 7i
⇒ Vậy số phức đang cho tất cả phần thực là 26; phần ảo là 7.
♦ các loại 2: màn biểu diễn hình học tập của số phức
- giải pháp giải: áp dụng điểm M(a;b) trình diễn số phức z trên mặt phẳng Oxy
° Ví dụ 1: Trong mặt phẳng toạ độ (hình vẽ dưới), số phức z = 3 - 4i được trình diễn bởi điểm nào trong các điểm A, B, C, D?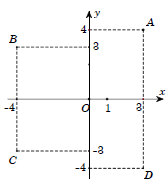
- Đáp án: Điểm D(3;-4) là trình diễn hình học của số phức z=3-4i
° Ví dụ 2: Số phức nào có màn biểu diễn hình học tập là toạ độ điểm M như hình sau: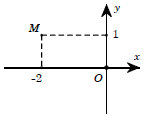
- Điểm M(-2;1) là trình diễn hình học của số phức z=-2+i
♦ loại 3: Tính Module của số phức
- biện pháp giải: đổi khác số phức về dạng z = a + bi ⇒ mô-đun là
° Ví dụ 1: tìm mô-đun của số phức sau:
° Lời giải:
- có
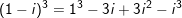
⇒ 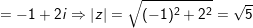
° Ví dụ 2: Cho số phức z vừa lòng 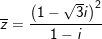
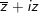
° Lời giải:
- Ta có:
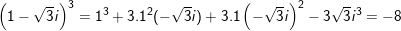
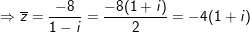
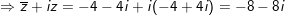
♦ nhiều loại 4: tra cứu số đối của số phức
- cách giải: biến đổi số phức về dạng z = a + bi ⇒ đối số của z là -z = -a - bi
° Ví dụ: Tìm số đối của số phức sau:
a)
b)
° Lời giải:
a)
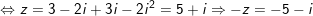
b)

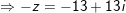
♦ nhiều loại 5: tìm số phức liên hợp của số phức z
- bí quyết giải: biến hóa số phức về dạng z = a + bi ⇒ số phức liên hợp của z là
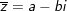
° Ví dụ 1: Tìm số phức liên hợp của số phức sau: 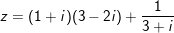
° Lời giải:
- Ta có: 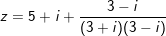
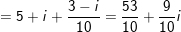
⇒ Số phức phối hợp của z là: 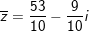
° Ví dụ 2: Cho z = a+ bi tìm số phức liên hợp của z và giải phương trình 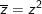
° Lời giải:
- Ta có 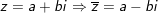
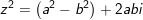
- khi đó: 
- Giải hệ này ta được các nghiệm 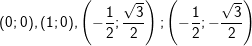
♦ loại 6: tìm số phức nghịch hòn đảo của số phức
- giải pháp giải: thực hiện công thức:
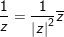
° Ví dụ : Tìm nghịch hòn đảo của số phức sau:
a)
b)
° Lời giải:
a)
- Ta có: 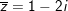


b)
- Ta có: 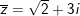
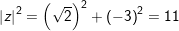
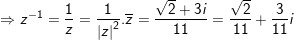
♦ Loại 7: Tìm những số thực lúc 2 số phức bởi nhau.
- giải pháp giải: sử dụng công thức:

° Ví dụ : Tìm các số nguyên x và y làm thế nào cho z = x + yi thỏa mãn z3 = 18 + 26i
° Lời giải:
- Ta có: 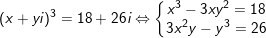
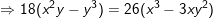
- Giải phương trình trên bằng phương pháp đặt y = tx (x≠0) ta được 
⇒ z = 3+ i
• Dạng 4: Tìm quỹ tích số phức (tập hợp những điểm) thoả mãn điều kiện cho trước.
* phương thức giải:
♦ nhiều loại 1: Số phức z toại ý về độ nhiều năm (module) khi đó ta sử dụng công thức
♦ loại 2: Số phức z là số thực (âm hoặc dương), khi ấy ta thực hiện kết quả
- Để z là số thực ⇔ b=0
- Đẻ z là số thực âm ⇔ a 0 và b = 0.
- Để z là số thuần ảo ⇔ a = 0.
° Ví dụ : Tìm tập đúng theo điểm M trình diễn số phức z thoả
a) 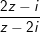
b) 
c) 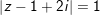
° Lời giải:
a) Gọi điểm M(x;y) ta có:

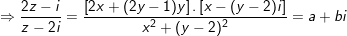
Với
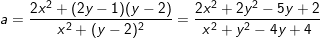
- Theo bài xích ra,
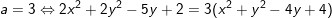
- với x ≠ 0 và y≠ 2 ta có:
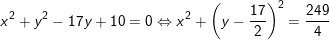
⇒ Vậy tập đúng theo điểm M là con đường tròn tâm
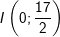
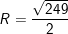
b) điện thoại tư vấn N là điểm biểu diễn số phức
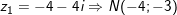
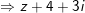
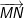
- Vậy quỹ tích của M là mặt đường thẳng qua N và song song với Ox, đó là đường thẳng y = -3.
c) gọi I là điểm biểu diễn của số phức
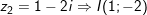
- khi đó:
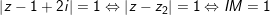
- Vậy quỹ tích của M là mặt đường tròn trung tâm I(1;-2) bán kính R = 1.
• Dạng 5: Chứng minh các biểu thức về số phức
* phương thức giải: Vận dụng các phép toán về số phức (cộng, trừ, nhân, chia, số phức liên hợp, mô-đun).
° Ví dụ 1: Cho số phức z thoả điều kiện . Triệu chứng minh 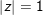
° Lời giải:
- Ta có: 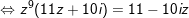
hay 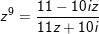
- Đặt z=x+yi, cùng với x,y ∈ R, tự (1) ta có:
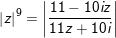
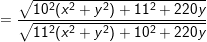
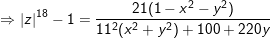
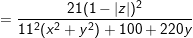
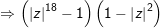
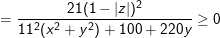
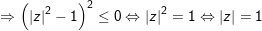
° Ví dụ 2: Cho 2 số phức z1 với z2 , chứng minh rằng:
a) 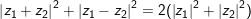
b) 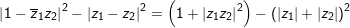
° Lời giải:
a) Ta có:
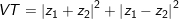
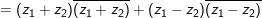
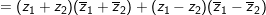
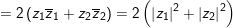
⇒ Vậy VT=VP (đpcm).
b) Ta có:
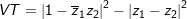
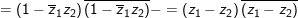
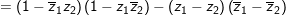
(1)
- khía cạnh khác:
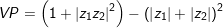

Vì 
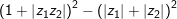
- trường đoản cú (1) và (2) bao gồm VT=VP (đpcm)
• Dạng 6: Căn bậc 2 của số phức với phương trình bậc 2
* phương pháp giải:
° Cho số phức: z = a + bi, số phức w = x + yi, được call là căn bậc 2 của số phức z ví như w2 = z tốt (x + yi)2 = a + bi.
- lưu lại ý:
♦ khi b = 0 thì z = a, ta gồm 2 ngôi trường hợp đơn giản sạ:
◊ TH1: a > 0 ⇒
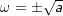
◊ TH1: a 2 = a + bi, hay x2 - y2 + 2xyi = a + bi
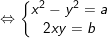
° Phương trình bậc 2 với hệ số phức
- Là phương trình gồm dạng: az2 + bz + c = 0, trong những số ấy a, b, c là các số phức a≠0
- biện pháp giải: Xét biệt thức
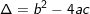
» Nếu Δ=0 phương trình tất cả nghiệp kép:
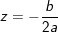
» Nếu Δ≠0 phương trình có 2 nghiệm phân biệt:
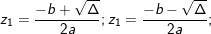
- Định lý Vi-ét: điện thoại tư vấn z1, z2 là 2 nghiệm của phương trình az2 + bz + c = 0 khi đó, ta có:

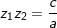
° Ví dụ 1: Tìm căn bậc 2 của số phức sau:
a) z = 5
b) z = -7
c)
* Lời giải:
a)
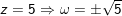
b)
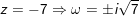
c) Gọi
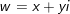
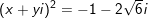
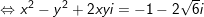
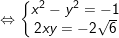
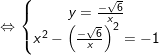

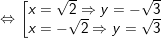
Vậy hệ pt trên có 2 nghiệm
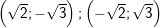
° Ví dụ 2: Trên tập số phức, search m nhằm phương trình bậc hai: z2 + mz + i = 0 (*) có với z1, z2 là nghiệm của (*).
* Lời giải:
- điện thoại tư vấn m=a+bi với a,b∈R.
- Theo bài toán, ta có:
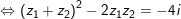
Theo Vi-ét: z1+z2=-m, z1z2=i nên:
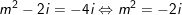
- Vậy ta có hệ:
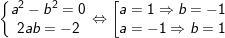
⇒ m=1-i hoặc m=-1+i.
° Ví dụ 3: Giải phương trình sau bên trên tập số phức:
a) z2 - 2z + 17 = 0
b) z2 + (2i+1)z + 1 - 5i = 0
c)
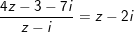
* Lời giải:
a) Ta có: z2 - 2z + 17 = 0 ⇔ z2 - 2z + 1 = -16 ⇔ (z + 1)2 = 16i2
⇔ (z + 1)2 = (4i)2 nên phương trình có 2 nghiệm phức: z1 = -1-4i; z2 = -1+4i
b) Ta có:

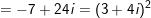
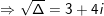
⇒ phương trình đã cho bao gồm 2 nghiệm z1=1+i; z2=-2-3i.
• Dạng 7: Phương trình quy về phương trình bậc 2
* cách thức giải: Đặt ẩn phụ và đem về phương trình bậc 2 tính Δ.
° Ví dụ 1: Giải phương trình phức sau:
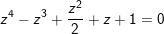
* Lời giải:
- nhấn thấy, z=0 chưa hẳn nghiệm của phương trình đề nghị chia 2 vế cho z2, ta được:
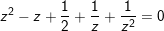
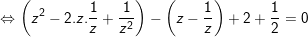
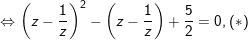
- Đặt
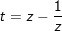

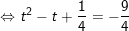

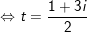

- với

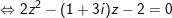
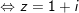
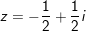
- cùng với
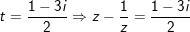
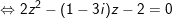
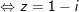
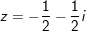
- Vậy phương trình (*) gồm 4 nghiệm:
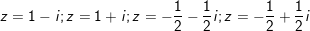
° Ví dụ 2: Giải những phương trình phức sau:
a)
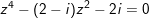
b)

c)
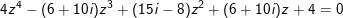
d)
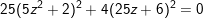
e)
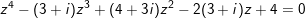
* Lời giải:
a) Đặt t = z2, lúc đó pt trở thành:
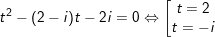
- Với
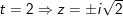
- Với
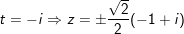
b) phân biệt z=0 chưa phải là nghiệm của phương trình phải chia 2 vế pt cho z2 ta được:
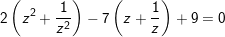
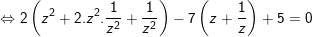
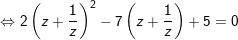
- Đặt
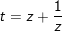
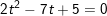
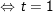

- Với
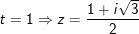
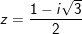
- Với
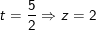
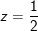
c) Đáp án:
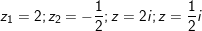
d) Đáp án:
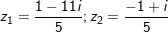

• Dạng 8: Dạng lượng giác của số phức
* phương thức giải:
° Công thức De - Moivre: Là công thức nền tảng cho hàng loạt công thức quan trọng đặc biệt khác như phép luỹ thừa, khai số phận phức, công thức Euler.
- công thức 1:
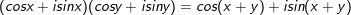
- công thức 2:

- Số phức z=a+bi ta có:
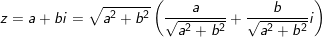
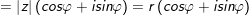
với
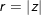
° Ví dụ 1: Viết những số phức sau bên dưới dạng lượng giác, từ kia hãy viết dạng đại số của z2012
a)
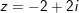
b)
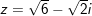
c)

* Lời giải:
a) Ta có:
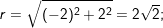

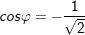
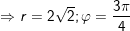
- Vậy
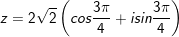
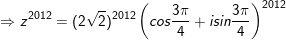
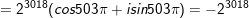
- Vậy z2012=-23018
b) Ta có:
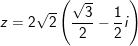
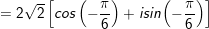
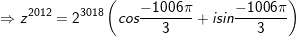
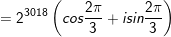
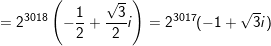
c) Ta có: